Algebra hrou


Úkoly

Výsledky:

  1. Z obrázku vidíme, že podle Pythagorovy věty 
              (AB)2 = 302 + x2
          (AC)2 = 202 + (50 - x)2.
    Avšak AB = AC, protože oba ptáci letěli stejnou rychlostí a letěli tutéž dobu.
    Proto 
              302 + x2 = 202 + (50 - x)2.
    obr
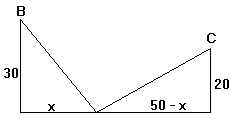
    Po odstranění závorek a po sloučení dostaneme jednoduchou rovnici 100x = 2000, takže x = 200.
    Ryba se objevila 20m od vyššího stromu nebo 30 m od nižšího stromu.
  2. Označme délu vlaku písmenem x a jeho rychlost písmenem y. Přejede-li vlak kolem pozorovatele za t1 sekund, ujede tedy vzdálenost x za t1 sekund. Jeho rychlost he tedy y = x/t1. Za t2 přejede a metrů dlouhý most, čili ujede vzdálenost, která se rovná délce mostu a délce vlaku. Rychlost v tomto případě bude y = (x + a)/t2.
    Z toho 
           x/t1 = (x + a)/t2,  x = at1/(t2 - t1)  a  y = a/(t2 - t1)
  3. Správné množství soli do pélvky označmíme jednotkou, protože nemůžeme určit, kolik je to, ale hledáme její část. Část této jednotky použité v prvním případě označme x. Z podmínek úlohy sestavíme rovnici: 
              2(1 - 2x) = 1 - x  ==>  x = 1/3.
    Do první polévky dal kuchař třetinu potřebného množství soli.
  4. Nechť objem nádov je V. Síla směsi v první nádobě po prvním přelévání 1 - x/V a po druhém přelevání (1 - x/V)2. Podobně síla v druhé nádobě po druhém přeléváním je (1 - 2x/V)2. Z podmínek úlohy platí: 16(1- x/V)2 = 25(1 - 2x/V)2 ==> x/V = 1/6.
    Z toho vyplívá, že x = 1/6 objemu nádoby.
  5. Číslici desítek označme písmenem x. Počet jednotek je o 3 větší, tedy x+3. V desítkové soustavě je možno toto číslo napsat takto: 10x + (x + 3). Po jeho zvětšení o 27 dostaneme: 10x + (x + 3) + 27. číslo s obráceným pořadím číslic je možno zapsat 10(x + 3) + x. Z podmínky platí: 
              10x + (x + 3) + 27 = 10(x + 3) + x,
          10x + x + 3 + 27 = 10x + x + 30.
    Po dalších úpravách dostáváme 0 = 0. Tato rovnost je zajisté správná, avšak nehovoří nic o hodnotě x. Znamená to tedy, že neexistují čísla, která by vyhovovala této úloze?
    Naopak, rovnice, kterou jsme sestavili, je správná pro jakoukoli neznámou hodnotu x. ?ůžeme se na konkrétních případech přesvědčit, že uvedenou vlastnost mají všechna dvojciferná čísla, v nichž je číslice jednotek o 3 větší než číslice desítek. 
              14 + 27 = 41,     47 + 27 = 74,
          25 + 27 = 52,     58 + 27 = 85,
          36 + 25 = 63,     69 + 27 = 96.
  6. Označme celou vzdálenost písmenem 2x kroků. Polovina této vzdálensti je tedy x kroků. Počet dvojkroků je x/2 a počet trojkroků x/3.
    x/2 - 250 = x/3; 3x - 1500 = 2x; x = 1500.
    Celá vzdálenost je 2x, tedy 3000 kroků.
  7. Označme čas, za který bodou oboje hodinky ukazovat stejný čas, písmenem x. bude to tedy, kdy se Štefanovy hodiny předběhnou a Gustavovy hodinky se zpozdí dohromady o 12 hodin (43 200 sekund). Štefanovy hodinky se za x hodin předbehnou proti správnému času o x sekund a Gustavovy za týž čas se zpozdí o 3/2 x sekund.
    Dostaváme rovnici 
              x + 3/2 x = 43200.
    Z toho x = 17280 hodin, čili 720dní.
    Štefan a Gustav by museli čekat téměř 2 roky, aby jejich hodinky ukazovaly opět tentýž čas.
    Ještě déle trvá, než hodinky ukážou správný čas. Štefanovy hodinky by se totiž musely předběhnout o 12 hodin a Gustovy by se museli o týž čas opozdit.
    Štefanovým hodinkám by to trvalo 43200 hodin, tj. 1800 dní, Gusstovým 3/2 krát kratší čas, tj. 1200 dní.
    Číslo, udávající počet dní, za které by současně oboje hodinky ukazovaly správný čas, musí být nejmenším společným násobkem čísel 1800 a 1200. Je to číslo 3600. Oboje hodinky budou tak ukazovat správný čas současně za 3600 dní, tj. téměř za 10 let.
  8. Jde o aritmetickou posloupnost, v niž první člen nechť je x, diference je 1,5. Patnáctý člen je potom x + 14 * 1,5 = x + 21.
    Víme, že patnáctý člen je osminásobkem prvního. Můžeme nyní sestavit jednoduchou rovnici x + 21 = 8x z toho x = 3.
    Stáří sourozenců bylo: 3; 4,5; 6; 7,5; 9; 10,5; 12; 13,5; 15; 16,5; 18; 19,5; 21; 22,5; 24 let.
  9. Jestliže eloktrické vozy opouštějí své konečné stanice každých x minut, znamená to, že za na místě, kde jsem se střatl s jedním vozem, přejede po x minutách následující vůz. Když mě vůz dožene, zanmená to, že za dobu 12 - x minut musel ujet tutéž vzdálenost, ketrou já ušel za 12 minut. Z toho vyplývá, že cestu, kterou ujdu za 1 minutu, ujede tramvaj za (12 - x)/12 minut. Jestliže vůz, jedoucí proti mně, semnou střetne za 4 minuty po tom, c jsem se střetl s předcházejícím vozem a ve zbývajících x - 4 minutách ujede tu cestu, kterou jsem já stačil ujít za 4 minuty, z toho opět vyplývá, že cestu, kterou já ujdu za jednu minutu, vůz ujede za (x - 4)/4 minut.
    Dostaneme rovnici: 
              (12 - x)/ 12 = (x - 4)/4
    Odkud x = 6. Tramvaje odjíždějí ze svých výchozích stanic každých 6 minut.
  10. Nakonec bylo v každé nádrži x hl ropy. Původně v nich bylo
    (x + 5) + (x - 3) + 0,5x + 3x = 46.
    Z toho 5,5x = 44 ==> x = 8.
    Nakonec bylo v každé nádrži 8 hl ropy.
  11. Jestliže číslici jednotek označíme písmenem x, můžeme číslici stovek vyjádřit výrazem x - a.
    V desítkové soustavě můžeme hledané číslo vyjádřit takto: 100(x - 4) + 7 * 10 + x.
    Číslo s opačným pořadím číslic bude: 100x + 70 + x - 4.
    Rozdíl těchto dvou čísel podle podmínky je
    (100x + 70 + x - 4) - [100(x - 4) + 70 + x] = 396;
    101x + 66 - 101x + 330 = 396;
    0 = 0.
    Uvedená rovnice je identitou a znamená, že každé trojciferné číslo, jehož první číslice je o 4 menší než třetí, zvětšuje se o 396, jestliže číslice napíšeme v opačném pořadí. (Číslice desítek nemá vliv na výsledek.)
  12. Ozančme si vzdálenost mezi dvěma městy písmenem d a průměrnou rychlost písmenem x. Potom platí: 
              2d/x = d/60 + d/40.
Po vynásobení  1/d dostaneme 
          2/x = 1/60 + 1/40.
    Po úpravě dostaneme 4800 = 40x + 60x, z toho x = 48. Tedy průměrná rychlost byla 48 km za hodinu a nikoli (60 + 40)/2 = 50 km za hodinu, jak by se na první pohled zdálo.
  13. Původní množství označíme písmenem x; potom první dostal: 
              x/2 + 1/2 = (x + 1)/2,
druhý dostal:
          1/2 [x - (x + 1)/2] + 1/2 = (x + 1)/22,
třetí dostal:
          1/2 [x - (x + 1)/2 - (x + 1)/4] + 1/2 = (x + 1)/23,
sedmý dostal:
          (x + 1)/27.
Máme rovnici:
          (x + 1)/2 + (x + 1)/23 + (x + 1)/23 + ... + 27
Z toho x/(x + 1) = 1 - 1/27; x= 27 - 1 = 127.
Všech jablek bylo 127.
  1. Jestliže věk Diofanta označíme x, jeho šestina je x/6, dvanáctinax/12, sedmina x/7 atd.
    Rovnice je jednoduchá: 
              x = x/6 + x/12 + x/7 + 5 + x/2 + 4
a z toho 
          x = 84.
    Diofantes žil 84 let. Z toho je možno lehce vypočítat, kdy se stal otcem, kdy ztratil syna apo.
  2. Tři za sebou jdoucí čísla zapíšeme: a, (a + 1), (a + 2). Jejich součet bude a + (a + 1) + (a + 2).
    Číslo dělitelné třemi zapíšeme 3k a součet všech čtyř čísel: 
              a + (a + 1) + (a + 2) + 3k = 3(a + k + 1).
    Když tento součet násobíme číslem 67, dostaneme 201(a + k + 1). a < 60, 3k < 100, čili k < 34. Výraz a + k + 1 není víc než dvojciferné číslo a součin 201 s libovolným jednociferným nebo dvojciferným číslem bude zakončeno tímto číslem. Výraz a + k + 1 předsatvuje číslo osledních dvou míst součinu (41). Jestliže od tohoto čísla odečteme známé číslo k + 1; (9 + 1), dostaneme číslo a, nejmenší ze tří na začátku zvolených čísel (41 - 10 = 31).
  3. 1. úvaha: V určitém okamžiku může být jeden dvakrát tak starý jako druhý. Jestliže je v tom okamžiku věk druhého x, je věk prvního 2x.
    První je o x roků starší než druhý. Tento rozdíl se stále zachovává.
    2. úvaha: V jiném okamžiku bude vk prvního tvořit 9/4 počtu let, kterého by druhý dosáhl v okamžiku uvedeném pod bodem 1.
    Úsečka zobrazující věk prvního musí být 9/4 x = 2 1/4 x a druhého bude zase o x menší, bude tedy 1 1/4 x.
    3. úvaha: Nynější počet let prvního je 15/16 počtu let druhého v okamžiku uvedeném v bodě 2, tj. 
              15/16 * 5/4 x = 75/64 x.
Věk druhého bude zase o x menší, bude tedy 
          75/64 - x = 11/64 x.
Protože dohromady je jim 86 let, platí
          75/64 x + 11/64 x = 86.
Z toho
          x = 64
    Prvnímu je tedy 75/64 * 64 = 75 let a druhému 11/64 * 64 = 11let.
  4. Označme věk Hlavatého písmenem x, počet dlaždic na jedné straně čtverce písmenem y. Dostaneme rovnici x2 - y2 = 1111. Číslo 1111 můžeme rozložit jediným možným způsobem na 101 * 11. Potom x2 - y2 = (x + y)(x - y) = 101 * 11 ==> x + y = 101; x - y = 11.
    Řešením soustavy rovnic dostaneme x = 56, y = 45. Tedy Hlavatému bylo 56 let, počet dlaždic po jedné straně čtverce je 45.

Úkoly
* Kurzy * Akcie * Práce * Zájezdy * Zájezdy * Meteobox * Auto *